Mathematics is full of mysteries that have fascinated humanity for thousands of years. Among the most intriguing are magic squares—arrangements of numbers in square grids where the sums of numbers in each row, column, and sometimes diagonals are equal. These enchanting number patterns have captivated mathematicians, artists, mystics, and puzzle enthusiasts alike, weaving a fascinating story across cultures and centuries.
In this article, we will delve into the history, construction, properties, and significance of magic squares and explore how number patterns beyond magic squares reveal deep mathematical beauty and connections.
What Is a Magic Square?
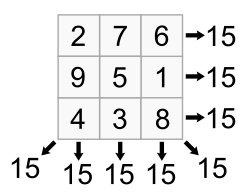
A magic square is a grid, typically square-shaped (n × n), filled with distinct positive integers such that the sums of the numbers in each row, column, and the two main diagonals are all the same. This constant sum is called the magic constant or magic sum.
For example, the simplest and most famous magic square is the 3×3 magic square using numbers 1 to 9:
| 8 | 1 | 6 |
|---|---|---|
| 3 | 5 | 7 |
| 4 | 9 | 2 |
Here, every row, column, and diagonal adds up to 15. For instance:
- Row 1: 8 + 1 + 6 = 15
- Column 2: 1 + 5 + 9 = 15
- Diagonal: 8 + 5 + 2 = 15
The magic sum for an n×n magic square filled with numbers 1 to n² can be calculated using the formula: M=n(n2+1)2M = \frac{n(n^2 + 1)}{2}M=2n(n2+1)
So, for the 3×3 case: M=3(9+1)2=3×102=15M = \frac{3(9 + 1)}{2} = \frac{3 \times 10}{2} = 15M=23(9+1)=23×10=15
A Brief History of Magic Squares
Magic squares have a long and rich history, tracing back thousands of years and crossing many cultures.
- Ancient China: The earliest recorded magic square is the Lo Shu Square, a 3×3 square discovered in Chinese legend around 2800 BCE. According to myth, the pattern was seen on the back of a turtle emerging from the Luo River. The Lo Shu Square has the same magic sum of 15 and is central to Chinese numerology and feng shui.
- India: Ancient Indian mathematicians and mystics studied magic squares extensively, incorporating them into religious and mystical contexts. The ancient Sanskrit text Kakuro references magic square concepts.
- Islamic World: Islamic mathematicians in the Middle Ages studied magic squares as well, linking them with astrology and talismans. Persian mathematician Al-Biruni and others wrote about the construction and properties of magic squares.
- Europe: Magic squares became a fascination in Renaissance Europe. Mathematicians and artists, such as Albrecht Dürer, included them in artworks. Dürer’s famous engraving Melencolia I (1514) features a 4×4 magic square, one of the earliest known depictions in Western art.
Types of Magic Squares
Magic squares come in many varieties:
1. Normal Magic Squares
These use the consecutive numbers from 1 to n² without repetition. The classic examples like the 3×3 and 4×4 squares belong to this category.
2. Panmagic Squares
Also called diabolic squares, these are magic squares where not only rows, columns, and main diagonals but also broken diagonals (wrap-around diagonals) add to the magic sum.
3. Associative Magic Squares
In these, each pair of numbers symmetric about the center sums to n² + 1. The 3×3 Lo Shu Square is associative.
4. Multiplicative Magic Squares
Instead of sums, the product of numbers in each row, column, and diagonal is the same.
Constructing Magic Squares
Constructing magic squares can be easy or challenging depending on their order (size).
Odd-Order Magic Squares (n is odd)
A classic method for constructing odd-order magic squares (3×3, 5×5, 7×7…) is the Siamese method or de la Loubere’s method:
- Start by placing the number 1 in the middle of the top row.
- Move up one row and right one column to place the next number.
- If this position is outside the square, wrap around to the opposite side.
- If the position is already occupied or you move out of the top-right corner, move one step down instead.
- Continue until all numbers are placed.
This simple algorithm reliably creates magic squares of any odd size.
Even-Order Magic Squares
Even-order squares are more complex, split into two cases:
- Doubly even (n divisible by 4): Special patterns or methods involving swapping certain positions.
- Singly even (n even but not divisible by 4): More intricate algorithms are required.
Number Patterns Beyond Magic Squares
Magic squares are a glimpse into the broader world of fascinating number patterns that have captivated mathematicians.
Arithmetic Progressions
Sequences where the difference between terms is constant. Examples include:
- 2, 4, 6, 8, 10 (difference 2)
- 5, 10, 15, 20 (difference 5)
These are foundational in understanding number patterns.
Geometric Progressions
Sequences where each term is multiplied by a fixed ratio:
- 3, 6, 12, 24, 48 (ratio 2)
- 5, 15, 45, 135 (ratio 3)
Pascal’s Triangle
A triangular array of binomial coefficients exhibiting patterns in sums, Fibonacci numbers, and even prime numbers.
Mathematical and Cultural Significance
Magic squares and number patterns are not just mathematical curiosities; they have rich cultural, mystical, and practical significance.
Mysticism and Symbolism
Throughout history, magic squares were associated with mystical and spiritual powers:
- In alchemy, certain magic squares were believed to contain magical properties.
- In Islamic culture, magic squares were used in talismans and amulets for protection or blessings.
- In Chinese tradition, the Lo Shu Square is linked to cosmic harmony and balance.
- In Western occultism, magic squares were tied to planetary magic and astrology.
Recreational Mathematics and Puzzles
Magic squares remain popular puzzles that develop logical reasoning, pattern recognition, and number sense. They are used in math education and competitions.
Applications in Modern Mathematics and Computing
- Error-Correcting Codes: Concepts from magic squares help in coding theory.
- Design of Experiments: Balanced arrangements inspired by magic squares improve statistical study designs.
- Cryptography: Some algorithms draw from number patterns to enhance encryption methods.
Examples of Fascinating Magic Squares
The Lo Shu Square (3×3)
| 4 | 9 | 2 |
|---|---|---|
| 3 | 5 | 7 |
| 8 | 1 | 6 |
Every row, column, and diagonal sums to 15.
Dürer’s Magic Square (4×4)
| 16 | 3 | 2 | 13 |
|---|---|---|---|
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
Challenges and Open Questions
Magic squares still pose challenges:
- How many magic squares exist for large n?
- Can we classify all types of magic squares?
- Are there undiscovered applications of magic squares in modern science?
Conclusion
Magic squares and number patterns are captivating intersections of art, mathematics, culture, and mystery. They reveal that numbers are not just abstract symbols but are woven deeply into the patterns of human thought and the natural world.
By exploring magic squares, we engage with a tradition thousands of years old that continues to inspire and challenge us. Whether you approach them as puzzles, mystical symbols, or mathematical objects, magic squares offer a window into the hidden beauty of numbers and patterns.